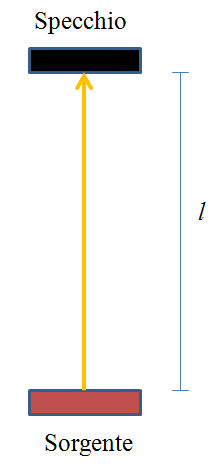Si sa che Einstein ha formulato una delle teorie più complesse e rivoluzionarie della storia della Fisica, la teoria della Relatività. Per i concetti rivoluzionari che esprime, affrontare la Relatività è un arduo e potenzialmente ingrato compito, ancor più per un non addetto ai lavori. Chi ha fatto studi scientifici, però, o anche chi è solo appassionato alla materia, non può non aver pensato almeno una volta – dopo la recente notizia della rilevazione delle onde gravitazionali – di volersi cimentare nell’impresa. Noi siamo qua, a provarci. Con questo articolo non proviamo a spiegare, perché per spiegare bisognerebbe padroneggiare la teoria, ma proviamo a capire.

Sfortunatamente, capire in modo approfondito è impossibile, se non con anni e anni di studi nel settore, così cerchiamo di farlo per quanto possibile, senza troppe pretese.

Tuttavia, chi con questo articolo spera di comprendere le onde gravitazionali rimarrà deluso, perché per ora la nostra attenzione andrà tutta sulla teoria della Relatività Ristretta. Ma non preoccupatevi, perché è difficilissima anche questa.

Per rendere la cosa un po’ meno scolastica e più dinamica, nonché per capire meglio, immagineremo un dialogo fra due personaggi: un curioso completamente a digiuno della teoria e un appassionato che ha tentato di capirci qualcosa.

Buon divertimento…e buona spremuta di meningi.

• Allora insomma oggi si parla della Ristretta.
• Devi camminare prima di correre. Non che questa sia facile, anzi.
• Bene. Mi ricordo qualcosa a proposito di velocità, tempo e spazio. Il tempo si deforma, oppure lo spazio…o tutt’e due?
• La terza. Per contestualizzare, ci dobbiamo ricordare al volo la composizione delle velocità nella relatività galileiana: in estrema sintesi, se io sono su un treno e tiro un sasso a una persona che sta per terra, ebbene quel sasso gli arriverà in testa a una velocità pari alla somma della velocità del treno più quella a cui io ho tirato il sasso.
• Cioè le due velocità si sommano.
• Esatto. Altro esempio veloce: se sono su un tapis-roulant, pur muovendomi resto fermo rispetto all’ambiente circostante, questo perché la velocità del tapis-roulant è uguale e opposta alla velocità a cui vado io con le mie gambe. Intuitivo no? Sotto gli occhi di tutti.
• Sì, il sasso sembra andare più veloce e io sembro stare fermo.
• No, non è che sembra. E’ proprio così, tant’è che un sasso lanciato da un treno ti ammazza. Cioè i due corpi, il sasso e io che cammino sul tapis-roulant, hanno energia diversa a seconda del sistema di riferimento.
• Energia relativa al sistema di riferimento. Già questa a pensarci bene mi sembra una cosa non banale.
• E neanche abbiamo sfiorato la Relatività di Enistein. Tutto filava liscio come l’olio finché nella seconda metà dell’Ottocento Maxwell non riunì in forma compatta le equazioni che descrivono l’elettromagnetismo. Per farla semplice, veniva fuori che il campo-elettromagnetico si propagava sotto forma di un’onda, l’onda elettromagnetica, a una velocità pari a quella della luce (circa 300’000 km/s).
• Non parleremo anche dell’elettromagnetismo, vero?
• Tranquillo, lo saltiamo a pie’ pari. Quello che interessa a noi è che veniva fuori una cosa molto strana, e cioè che nell’equazione d’onda del campo-elettromagnetico la velocità di propagazione – la velocità della luce appunto – era una costante.
• E cosa c’è di strano? E costante in che senso, rispetto a cosa?
• Rispetto a tutto. Di strano c’era che questo risultato era in apparente contraddizione con il discorso di prima del treno, del sasso e del tapis-roulant. Cioè se la velocità della luce è costante, questo significa che se invece di tirare dal treno un sasso, “tiro” un raggio di luce, questo va comunque alla stessa velocità per chi è a terra. Quindi, o la luce ha qualcosa di particolare, oppure la relatività galileiana è sbagliata.
• Cioè se si salvava la teoria di Maxwell non funzionava la relatività galileiana, e viceversa?
• Esatto. In particolare, salvando la composizione delle velocità di Galilei, le equazioni di Maxwell dovevano essere adattate volta per volta al sistema di riferimento da cui si descriveva il fenomeno elettromagnetico. In altre parole, mantenere la vecchia meccanica comportava che le formule di Maxwell avessero forma diversa al variare del sistema di riferimento.
• In che senso “forma diversa”? E in che senso al variare del sistema di riferimento?
• Per farla breve, diciamo che le costanti delle equazioni cambiano al variare del sistema di riferimento, invece di rimanere, appunto, costanti.
• Ok. Non ho capito però perché le leggi di Maxwell cambierebbero forma.
• Per capire perché le leggi di Maxwell si pensava cambiassero forma bisogna dire che nella seconda metà dell’Ottocento si credeva che l’onda elettromagnetica, come tutte le onde, si propagasse attraverso un mezzo, chiamato etere luminifero, e che quindi si muovesse a una certa velocità – quella della luce – proprio in quel mezzo privilegiato. Di conseguenza qualsiasi riferimento in moto rispetto a questo fantomatico etere avrebbe rilevato una velocità della luce diversa. Velocità della luce diversa al variare del sistema di riferimento significa velocità della luce variabile anche nelle equazioni di Maxwell a seconda, appunto, del sistema di riferimento. Cosa che non veniva contemplata dalla teoria, in cui compariva come una costante.
• Aspetta ma non ho capito bene questo etere, è un po’ come l’aria per il suono, per capirci?
• Cioè?
• Be’ il suono si propaga con una certa velocità (circa 340 m/s in particolari condizioni di pressione e temperatura) nell’aria “ferma”, a prescindere dalla mia velocità. Cioè se io sto su un treno, mi affaccio dal finestrino e lancio un urlo – effetti doppler a parte – quel suono si propaga comunque a circa 340 m/s per te che sei a terra, perché si propaga nell’aria “ferma”.
• Sì, una cosa simile. L’equivalente dell’aria per molto tempo i fisici credettero fosse l’etere. Con una differenza però: se sono sul treno e invece di affacciarmi dal finestrino rimango nella cabina – al chiuso – la cabina trasporta con sé dell’aria, e se lancio un urlo questo si propagherà all’interno di essa a circa 340 m/s. Di conseguenza, per uno che sta per terra, il suono si muoverà a 340 m/s più la velocità del treno.
• E per l’etere non funzionava così?
• No, perché l’etere si pensava fosse imperturbabile, incontenibile, e che non offrisse nessuna resistenza.
• Ok. Quindi come un’aria che pervade tutto ma è sempre “ferma”.
• Esatto. Questo faceva nascere una questione…
• Come è possibile che esista un sistema di riferimento assoluto?
• Einstein sarebbe fiero di te, ma a dir la verità la domanda che ci si fece all’inizio fu molto più “banale”.
• A che velocità andiamo rispetto all’etere?
• Una mezza specie. Tanto che Michelson e Morley fecero un esperimento che è rimasto nella storia: avendo ipotizzato la Terra in movimento rispetto all’etere, che permeava l’universo, pensarono che misurando la velocità della luce in diverse direzioni avrebbero intercettato il moto di rotazione e quello di rivoluzione della Terra stessa, e quindi avrebbero trovato delle differenze.
• Aspetta aspetta vai piano…riprendiamo l’esempio del treno. Supponiamo che sono su un vagone all’aperto, quindi sento un “vento” dovuto al fatto che vado incontro all’aria. Se avessi un dispositivo in grado di misurare la velocità del suono dovrei misurare, sul treno, una velocità del suono minore?
• Esatto. Perché il suono si propaga nell’aria “ferma” che, nel sistema di riferimento del treno, ha una velocità uguale e opposta a quella del treno stesso (il “vento” di cui parli tu). Solo che nell’esperimento di Michelson e Morley in gioco c’erano le velocità dovute alla rotazione e alla rivoluzione terrestri. Etere “fermo” (per capirci), e Terra in movimento. L’etere è l’aria e la Terra è il treno: a seconda di come oriento la luce dovrei misurare velocità diverse.
• Ci sta. Aspetta però…e che mi dici delle altre velocità?
• Quali velocità?
• Be’ quella del sistema solare per esempio, quella della galassia, del sistema di galassie…cioè se l’etere era davvero “assoluto”, avrebbero dovuto aspettarsi di misurare anche le velocità di sistema solare e galassia, no? E quella del sistema di galassie, e così via. Oppure pensavano che l’etere fosse solidale al sistema solare?
• Bella domanda. Bel casino. Diciamo che non credo di dire stupidaggini se dico che in quel periodo (si parla di fine Ottocento, e la scoperta dell’espansione dell’Universo è del 1929) pensavano che il sistema solare fosse fermo, e cioè che, a questo punto è lecito pensarlo, coincidesse proprio con il sistema privilegiato dell’etere.
• Be’ lasciamo stare che è meglio. Ma insomma che velocità trovarono?
• Sempre la stessa. In ogni direzione, sempre la velocità della luce c.
• Ma magari avevano degli strumenti che non riuscivano ad apprezzare la differenza! La Terra ha una velocità tangenziale dovuta alla rotazione di 460 m/s all’equatore e di 30 km/s per la rivoluzione: sono numeri piccoli se confrontati a 300’000 km/s.
• No. Anzi avevano uno strumento capace di apprezzare uno scarto ben minore. Solo che non trovarono nessuna differenza.
• Va bene. Quindi in sostanza questo esperimento doveva dimostrare l’esistenza dell’etere, rilevando la velocità relativa della Terra, invece finì per metterla in crisi?
• Non proprio. Però sicuramente, anche mantenendo l’ipotesi dell’esistenza di un etere, si doveva rivedere il concetto di composizione delle velocità.
• Quindi di una cosa siamo certi: Maxwell aveva ragione e la luce è costante in tutti i sistemi di riferimento.
• Sì. C’era anche e soprattutto l’esperimento di Fizeau sul trascinamento della luce nell’acqua in movimento a dimostrarlo: la luce non rispettava la composizione delle velocità per come l’abbiamo vista finora, e la sua velocità è uguale in tutti i sistemi di riferimento.
• Ok. Quindi io sto su un treno e ho con me un dispositivo accuratissimo in grado di misurare la velocità della luce. Se una torcia, ferma a terra, mi invia dei lampi di luce io misurerò la stessa velocità sia che mi trovi sul treno sia che mi trovi a terra, per quanto il treno vada veloce.
• Esatto. Strano no? Ma verificato sperimentalmente.
• Direi. Quindi ripartiamo da qui: abbiamo da una parte la teoria di Maxwell sull’elettromagnetismo e dall’altra la relatività galileiana. Le equazioni di Maxwell sono salve, perché la luce abbiamo visto essere costante in tutti i sistemi di riferimento e quindi le leggi non cambiano forma al variare del sistema di riferimento. La relatività di Galilei invece ne esce con le ossa rotte, giusto?
• Già.
• E quindi andavano cambiate le leggi della meccanica.
• Sì.
• Ma l’etere lo abbiamo fatto fuori?
• Non ancora. Come detto, l’esperimento di Michelson e Morley non demoliva necessariamente l’idea di etere, e negli ultimi anni dell’Ottocento e nei primissimi del Novecento i suoi sostenitori erano ancora in tanti. Tra questi, c’era Lorentz.
• Lorentz? Ma quando arriva Einstein?
• Tra un po’. Ma vale la pena vedere tutti gli antefatti alla sua teoria, perché questo aiuta a capire la teoria stessa. Lorentz credeva ancora in un sistema di riferimento assoluto, l’etere appunto, e tirò fuori le famose trasformazioni – le stesse della teoria della relatività – proprio per salvare il concetto di etere:da notare la differenza con le trasformazioni di Galilei:
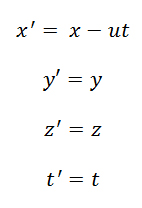
• Ma io queste formule le ho già viste a proposito della Relatività di Einstein. Come è possibile che tirò fuori le stesse trasformazioni della Relatività?
• Perché queste equazioni vengono fuori se si impone la costanza della velocità della luce in tutti i sistemi di riferimento, che sarà uno dei postulati della teoria di Einstein. Einstein le dimostrerà autonomamente nel suo articolo del 1905.
• Cosa rappresentano?
• Confrontano le coordinate di un punto a un determinato tempo in due sistemi di riferimento in moto a velocità u l’uno rispetto all’altro. Lorentz identificava uno dei due sistemi, quello senza apici (x, y, z e t), col sistema di riferimento privilegiato dell’etere.
• Perché in questo modo l’etere si salvava?
• L’idea di Lorentz era che Michelson e Morley avessero rilevato la stessa velocità della luce perché i bracci meccanici dell’apparato sperimentale si restringevano nella direzione del movimento terrestre, e le sue equazioni lo rappresentavano matematicamente.
• Ah, quindi secondo Lorentz Michelson e Morley avevano misurato la stessa velocità perché la luce, a velocità minore, aveva compiuto anche uno spazio minore. Ma che significato fisico dette a queste trasformazioni? Perché altrimenti sono solo un artificio matematico per far tornare i conti. In altre parole, come spiegava questa contrazione dal punto di vista fisico?
• Lorentz ipotizzò che fossero le forze elettromagnetiche a tenere insieme le particelle di un corpo, e a determinarne forma e dimensioni. Penso, così, che muovendosi nell’etere gli oggetti mutassero le proprie dimensioni nella direzione del movimento proprio a causa del mutamento delle forze elettromagnetiche.
• Ok, quindi questo ragionamento spiegava la deformazione spaziale. Ma per quanto riguarda il tempo? Vedo un’espressione particolare anche per il tempo…
• Lorentz chiamò il tempo t’ tempo locale. Tuttavia, per il fisico olandese rimaneva un mero artificio matematico, e non gli diede mai una spiegazione fisica, perché credeva in un tempo assoluto di stampo newtoniano.
• Ma a quanto pare si sbagliava. Finalmente arriviamo a Einstein?
• Ci siamo. Einstein era convinto che le leggi di Maxwell, e della Fisica in generale, dovessero essere le stesse in tutti i sistemi di riferimento inerziali (anni più tardi riuscirà a estendere questo principio anche a quelli non inerziali), se non sbaglio per la convinzione che la natura si potesse descrivere in modo semplice. Per cui il primo postulato della teoria della relatività ristretta è: tutte le leggi fisiche sono le stesse in tutti i sistemi di riferimento inerziali.
• Ok, quindi le equazioni di Maxwell rimangono le stesse, e le equazioni della meccanica diventano quelle di Lorentz.
• Sì. Solo che diversamente da Lorentz Einstein non credeva nell’etere, e diede una spiegazione fisica alle trasformazioni, demolendo le concezioni di spazio e tempo assoluti.
• Sono proprio curioso di sentire come…
• Qua il gioco si fa duro. L’esempio è di Feynman (Sei pezzi meno facili), non è di Einstein, ma fa capire bene il concetto. Supponiamo di avere sempre il solito treno che va ad altissima velocità. Identifichiamo il treno con un sistema di riferimento K’ e un osservatore “fermo” con il sistema di riferimento K. Ora supponiamo di avere montato sul treno un orologio particolare, costituito da una sorgente di luce e da uno specchio posto di fronte a essa a una distanza l:

• Come funziona di preciso questo orologio?
• La luce parte dalla sorgente, rimbalza sullo specchio e ritorna vero la sorgente. Consideriamo andata e ritorno come un’unità di tempo, un ticchettio, che se misurato nel sistema di riferimento del treno sarà pari a: E’ importante precisare che l’orologio è disposto perpendicolarmente al moto del treno. Ora consideriamo di guardare, stando a terra, l’orologio che si trova sul treno, che abbiamo detto andare ipoteticamente ad altissima velocità, supponiamo cioè di osservare l’orologio dal sistema di riferimento K. Vedremo questo (u è la velocità del treno):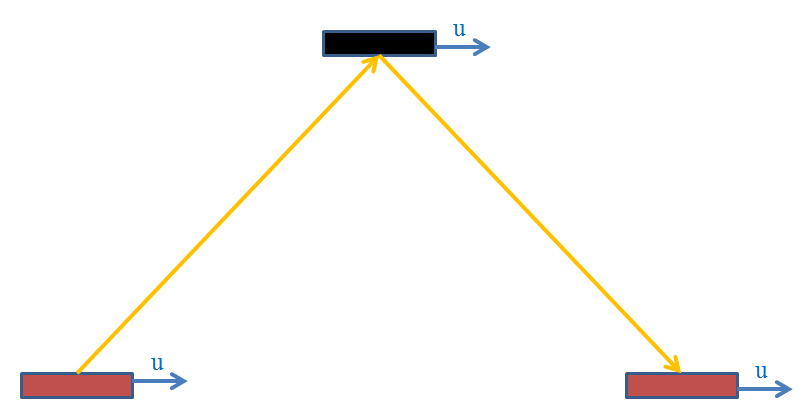Quindi la luce deve percorrere uno spazio maggiore per arrivare allo specchio e ritornare.
• Ma questo vale sempre! Cosa aggiunge di nuovo la Relatività Ristretta?
• La differenza sta nel fatto che se andiamo a calcolare la velocità del raggio di luce – visto dal sistema di riferimento “fermo” – dovremo farlo come spazio percorso diviso tempo. Ma noi sappiamo – per tutto ciò che abbiamo detto finora –  che questo valore deve essere uguale a c, qualsiasi sia il moto dell’orologio. Facendo riferimento alla figura seguente: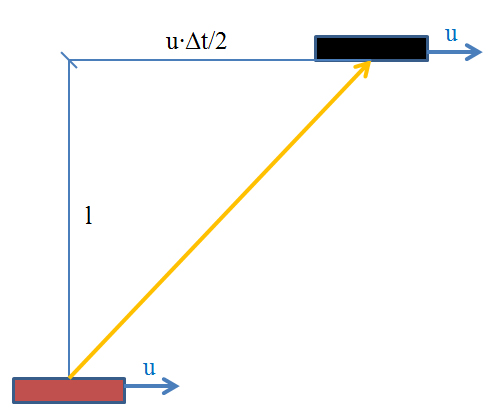avremo quindi:Facendo qualche calcolo, e ricordando la definizione di Δt con zero, arriviamo a:da cui un tempo maggiore rispetto a quello misurato dall’orologio sul treno, di un fattore crescente con la velocità u, detto fattore di Lorentz. Se restassimo fermi alla Relatività Galileiana, invece, calcoleremmo una velocità della luce maggiore di c (in accordo con la regola del parallelogramma per la somma tra le velocità del treno e del raggio di luce), non riscontrando nessuna dilatazione dei tempi.
• Ma questo funziona solo con la luce?
• No, non succede solo per la luce. Ci serviamo della luce in questo esempio perché è comodo: se usassimo qualcosa di diverso dall’onda elettromagnetica – per esempio un proiettile – dovremmo applicare la composizione relativistica delle velocità per calcolare la velocità risultante del proiettile, con evidenti difficoltà in più, ma il risultato non cambierebbe: avremmo comunque lo stesso sfasamento dei tempi.
• Composizione relativistica delle velocità?
• Ne parliamo dopo. Possiamo dimostrare questo stesso risultato anche matematicamente maneggiando le equazioni di Lorentz. Volendo descrivere il tempo dell’orologio sul treno avremo che esso, per un osservatore fermo, viaggia proprio alla velocità del treno, cioè u. La sua equazione del moto sarà quindi: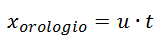che sostituita nell’espressione del tempo t’ dà:da cui:
• Praticamente mi stai dicendo che un fenomeno osservato in sistemi di riferimento in moto l’uno rispetto all’altro ha diversa durata.
• Sì, il tempo scorre diversamente a seconda del sistema di riferimento.
• A dirla tutta non sono per niente convinto. Peraltro l’espressione “il tempo scorre diversamente” è diversa da “un fenomeno ha diversa durata”, e mi lascia perplesso. Ci si arriva matematicamente, e va bene. Nell’esperimento mentale dell’orologio, però, abbiamo qualcosa che si muove nello spazio, ed è diversa la misura del suo moto. Perché mai questo dovrebbe aver a che fare con lo scorrere del tempo inteso nella sua accezione generale? Che mi dici per esempio del tempo biologico?
• Osservazione più che lecita. Tuttavia nasconde una non profonda comprensione dell’esperimento mentale che abbiamo condotto, e permette d’altro canto di giungere al senso profondo della teoria della Relatività Ristretta. Il punto è che questo esperimento quantifica soltanto la dilatazione dei tempi, partendo dall’assunto che la velocità della luce deve essere sempre la stessa in tutti i sistemi di riferimento. In altri termini, non si ha una misura dilatata dei tempi perché l’orologio è a luce e la velocità della luce è costante, è il contrario: si ha una velocità della luce costante perché i tempi si dilatano. Questo è il rivoluzionario capovolgimento del ragionamento che conduce Einstein, e questa è la differenza con Lorentz: non è necessario ammettere l’esistenza di un etere e trovare teorie astruse per dire che la velocità della luce è la stessa, se si ammette che sono lo spazio e il tempo a deformarsi a seconda del sistema di riferimento. L’unico postulato della teoria della Relatività Ristretta è, infatti, che le leggi fisiche sono le stesse in tutti i sistemi di riferimento inerziali. La costanza della velocità della luce è solo una conseguenza (sebbene Einstein l’abbia posta all’inizio come secondo postulato). Infatti ci serviamo della luce nell’esempio dell’orologio solo perché è facile, ma se usassimo qualcosa di diverso dall’onda elettromagnetica otterremmo comunque lo stesso risultato.
• Continuo a non essere convinto. Mi sembra assurdo che, per esempio, si invecchi diversamente a seconda del sistema di riferimento.
• Affidiamoci a Feynman allora (tratto da Sei pezzi meno facili):

Se la teoria della relatività è corretta [il rallentamento] non riguarda solo questo particolare tipo di orologio [a luce]: ogni orologio, su qualunque principio si basi, sembrerebbe rallentare della stessa misura. Come mai è così? Per rispondere a questa domanda supponiamo di avere altri due orologi fatti esattamente allo stesso modo – con ruote o ingranaggi, o magari basati sul decadimento radioattivo o su qualcos’altro – e di sincronizzarli esattamente con i primi due. Quando in un orologio a luce un raggio va avanti e indietro segnalando il suo arrivo con un clic, anche i nuovi modelli completano una qualche forma di ciclo, che annunciano simultaneamente con lampi, suoni, o altri segnali. Uno dei nuovi orologi va nella navicella spaziale [il nostro treno] insieme a quello del primo tipo. Chissà, magari questo orologio, anziché rallentare, continuerà a tenere lo stesso ritmo del suo gemello a terra, in disaccordo con l’altro modello nella navicella… Eh no! Se così fosse l’astronauta potrebbe usare lo sfasamento dei suoi due orologi per determinare la velocità della navicella, ma noi abbiamo supposto che ciò sia impossibile. Non è necessario sapere nulla sul meccanismo del nuovo orologio che potrebbe indurre il rallentamento – sappiamo già che, quale che ne sia la ragione, rallenterà come il primo. Ma se tutti gli orologi in movimento vanno più piano, se in ogni tipo di misura del tempo non si ottiene altro che un ritmo più lento, dovremo ammettere che, in un certo senso, è il tempo stesso a rallentare. Tutti i fenomeni – le pulsazioni del cuore, i processi mentali, il tempo per crescere e invecchiare – devono rallentare in proporzione, perché l’uomo non può dire se è in movimento o meno.

• Cosa intende quando dice: “Se così fosse l’astronauta potrebbe usare lo sfasamento dei suoi due orologi per determinare la velocità della navicella, ma noi abbiamo supposto che ciò sia impossibile”?
• Abbiamo detto che secondo la teoria le leggi che descrivono i fenomeni fisici hanno la stessa forma in tutti i sistemi di riferimento. Questo rende impossibile stabilire, non guardando all’esterno della cabina di un treno o di una navicella, se si è in movimento o meno.
• In effetti anche la Terra è in movimento. Perché quel particolare orologio a cui fa riferimento Feynman su una navicella dovrebbe continuare a segnare proprio “l’ora della Terra”? Ciò farebbe della Terra un sistema di riferimento privilegiato, ma appunto anche la Terra è in movimento, e anche il sistema solare, la galassia, e così via. Prendere uno di questi come sistema in cui scorre un tempo assoluto non ha senso. Questo tuttavia, dal punto di vista logico, non esclude un sistema di riferimento assoluto, o sbaglio?
• No, ma non lo rende necessario. Infatti Einstein all’inizio negò l’esistenza dell’etere, ma in una lettera a Lorentz rettificherà così:

“Sarebbe stato più corretto se nelle mie prime pubblicazioni mi fossi limitato a sottolineare l’impossibilità di misurare la velocità dell’etere, invece di sostenere soprattutto la sua non esistenza. Ora comprendo che con la parola etere non si intende nient’altro che la necessità di rappresentare lo spazio come portatore di proprietà fisiche.”

• La seconda parte non l’ho capita.
• Neanche io. Magari però l’ha capita qualcuno che ascolta.
• Ma il fatto che non si possa stabilire, senza guardare fuori dal treno o dalla navicella, se ci si trovi in movimento non lo diceva anche la Relatività Galileiana?
• Sì, infatti la Relatività Ristretta è un’estensione della Galileiana alle leggi fisiche sui fenomeni elettromagnetici.
• Comincio a convincermi. Cosa succede invece se orientiamo l’orologio nella direzione del moto del treno?
• Un gran caos.
• Non dovremmo misurare lo stesso sfasamento dei tempi? E’ pur sempre un orologio, è solo orientato diversamente.
• Infatti misuriamo lo stesso sfasamento. Tuttavia, questo è possibile solo se si ammette una contrazione delle lunghezze, la stessa a cui si riferiva Lorentz a proposito dell’esperimento di Michelson e Morley. La teoria prevede infatti che le dimensioni spaziali parallele alla direzione del moto si restringano secondo questa relazione: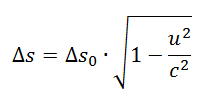dove con Δs con zero indichiamo la lunghezza propria di un oggetto, misurata nel sistema di riferimento in cui l’oggetto è fermo.
• Questa come si spiega?
• Spiegare questa con un esempio è più difficile. Supponiamo di avere un orologio simile al precedente, ma stavolta il raggio di luce invece che riflettersi su uno specchio solidale alla sorgente si riflette su un treno fatto di specchi, e animato da una velocità u.
• Un treno fatto di specchi?
• Sì, un treno che abbia su un lato una serie di pannelli l’uno adiacente all’altro. Ora supponiamo, senza perdere di generalità (dal momento che potremmo scegliere a piacimento una dimensione degli specchi diversa) che il raggio di luce parta dalla sorgente quando un’estremità dello specchio si trova in corrispondenza della sorgente stessa, e che ritorni alla sorgente quando sia l’altra estremità a trovarsi in corrispondenza della sorgente. In pratica supponiamo di avere l’orologio a luce sincronizzato con la frequenza di passaggio dei pannelli a specchio sul treno: la velocità del treno sarà la lunghezza del pannello Δs diviso la durata di un ticchettio Δt. 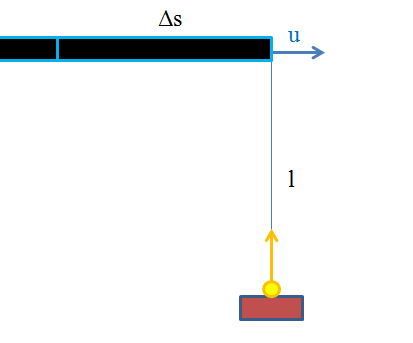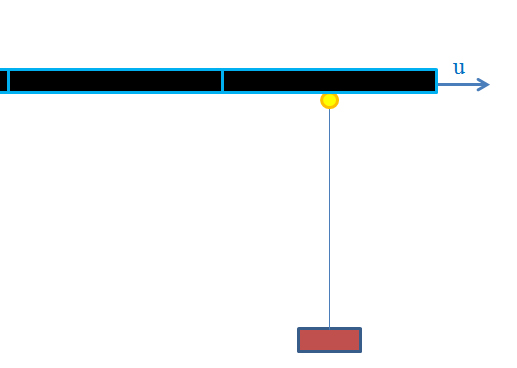Dal sistema di riferimento della sorgente vedremo:Avremo quindi:Nel sistema di riferimento del treno vedremo, invece: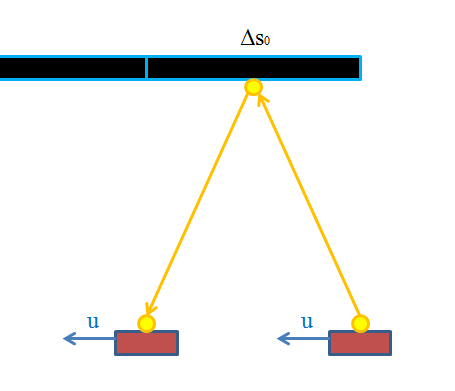Per cui la misura del pannello sarà data dallo spazio percorso dalla sorgente (Δs con zero perché è la misura dell’oggetto nel sistema di riferimento in cui l’oggetto stesso è fermo):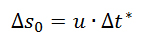Solo che l’intervallo di tempo sarà diverso dal Δt di prima, e uguale al tempo che impiega la luce a percorrere lo spazio rappresentato in figura:da cui, ricordando che 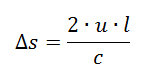si ottiene: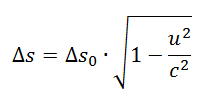Anche questa si può derivare matematicamente – per la verità in modo più facile – dalle equazioni di Lorentz. Riprendiamo l’espressione che lega le coordinate di un punto nei due sistemi di riferimento K e K’ in moto rispetto a K con velocità u: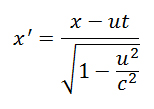e considerando i due estremi di un segmento, i punti 1 e 2, abbiamo: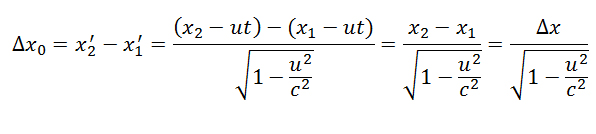avendo ipotizzato il segmento fermo nel sistema di riferimento K’, il quale misura quindi Δx con zero.
• Bene, bene. Prima o poi (più poi che prima) mi vedrò per bene queste dimostrazioni. Il succo è che un oggetto misurato nel sistema di riferimento in cui è fermo non subirà distorsioni, ma se si muove subirà una contrazione nella direzione del moto. Ma questo effetto è apparente o reale?
• E’ reale come è reale il fatto che un sasso lanciato da un treno ti ammazzi. Riprendendo quello che abbiamo detto all’inizio, come un sasso lasciato cadere da un treno ha una certa energia rispetto a chi è fermo perché si trova su un treno in movimento, così, per il fatto di essere in movimento, qualsiasi cosa subirà la contrazione delle lunghezze (e la dilatazione dei tempi).
• Quindi è un fenomeno non riscontrabile da chi si trova nel sistema di riferimento in movimento, giusto?
• No. Come abbiamo detto, qualora l’osservatore in movimento misurasse, nel suo sistema di riferimento, la durata di un fenomeno o la lunghezza di un oggetto lo farebbe con il suo orologio e con il suo metro, non rilevando quindi differenze.
• Mi stanno nascendo una serie di dubbi piuttosto inquietanti…
• Tipo?
• Tipo, per esempio: dalle equazioni si vede come la velocità della luce sia un limite superiore insuperabile, a meno di ammettere tempi e distanze immaginarie. Bene…quindi è un valore insuperabile, ma rispetto a chi?
• Spiegati meglio.
• Supponiamo che io sulla Terra mi avvicini tantissimo alla velocità della luce, per esempio con un acceleratore di particelle. La Terra però è in movimento, e – come abbiamo già detto – non solo la Terra ma il sistema solare, la galassia, ecc. Ora supponiamo, per un attimo, di spostarci su un pianeta in un’altra galassia, rispetto alla quale la Terra, insieme a tutta la Via Lattea, viaggia ad altissima velocità, e supponiamo – per quanto sia improbabile – che rispetto al pianeta nell’altra galassia la velocità della Terra e quella della particella nell’acceleratore siano parallele, il che non è escluso che capiti davvero, seppur per un tempo limitato. Se io mi trovassi su questo pianeta nell’altra galassia non vedrei forse la particella superare la velocità della luce?
• No. Per quanto assurdo possa sembrare e per quanto la particella e le galassie vadano veloci la velocità della particella si avvicinerebbe tantissimo a quella della luce senza mai raggiungerla: la Relatività ha introdotto, infatti, una nuova legge di composizione delle velocità. Per dimostrarla dobbiamo riprendere le espressioni di Lorentz per spazio e tempo ed esplicitarle rispetto a x e t anziché rispetto a x’ e a t’, il che non è immediato e richiede delle noiose sostituzioni che non è il caso di mostrare:Per arrivarci concettualmente basta pensare che chi si trova nel sistema di riferimento che finora abbiamo considerato in moto con velocità u può dire, al contrario, che sia l’altro sistema di riferimento a muoversi di velocità – u, da cui la stessa forma delle trasformazioni ma con il segno della velocità u opposto. Ora pensiamo che invece di essere fermo il punto individuato dalla coordinata x e x’ si muova di velocità v e v’. 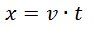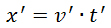Avremo che le equazioni del moto nei rispettivi sistemi di riferimento saranno:esostituendo queste espressioni nelle equazioni scritte sopra si ottiene, dopo qualche noiosissimo calcolo: contro la legge di composizione galileiana delle velocità, che prescriveva una semplice addizione:
• Ok. Ritornando al mio esempio?
• Ritornando al tuo esempio, se ci posizioniamo nel sistema di riferimento del pianeta nell’altra galassia u è la velocità della Terra rispetto al pianeta, v’ la velocità della particella misurato nel sistema di riferimento della Terra, e v la velocità della particella misurata dal pianeta (cioè la velocità che vogliamo misurare e che tu presumi superiore a quella della luce)
• Ok, proviamo. Supponiamo che la Terra vada a 200’000 km/s rispetto al pianeta nell’altra galassia e la particella vada a 250’000 km/s sulla Terra…
• Avremo:contro i 450’000 km/s che direbbe la relatività galileiana.
• Viene comunque inferiore alla velocità della luce! E se invece della particella voglio misurare proprio la velocità di un raggio di luce?
• Otterresti quello che andiamo dicendo dall’inizio: sempre la velocità della luce. Provare per credere.
• Quindi se ritorniamo alla mia domanda iniziale: la velocità della luce è un limite superiore insuperabile, ma rispetto a chi? La risposta dovrebbe essere: rispetto a qualsiasi cosa. Giusto?
• Credo proprio di sì.
• Quindi tutto è relativo, ma mica poi così tanto. Abbiamo un limite insuperabile, che è la velocità della luce, una costante in tutti i sistemi di riferimento – la velocità delle onde elettromagnetiche – e poi abbiamo che tutte le leggi della fisica sono le stesse in tutti i sistemi di riferimento. O sbaglio?
• Per niente. Infatti sono in molti a sostenere che il nome “Relatività” non sia adatto alla teoria di Einstein. A dirla tutta, oltre alle quantità che hai citato, ce n’è un’altra che non varia mai al mutare del sistema di riferimento: quello che si chiama intervallo invariante, o invariante spazio-temporale.
• Lo sapevo. Pensavo di cavarmela senza lo spazio-tempo.
• Ci tocca. Con la teoria di Einstein si è reso necessario abbandonare le concezioni distinte di spazio e tempo, e riunirle in un unica entità: lo spazio-tempo, appunto. Non solo, ma si sostituisce all’idea di punto spaziale il concetto di evento spazio-temporale.
• Perché? Perché non si possono più considerare spazio e tempo come entità separate?
• Per cominciare, pensiamo che fino alla Relatività si era convinti che in qualunque sistema di riferimento la misura della distanza tra due punti fosse invariante. Così non è.
• Un esempio al volo?
• Facendo riferimento all’immagine seguente: prendiamo un segmento AB in un sistema di riferimento K’ in moto rispetto a K con velocità u. Chiamando l la lunghezza del segmento AB, misurata nel sistema di riferimento K’, possiamo scrivere: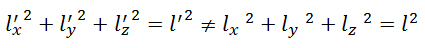 cioè la lunghezza misurata in K’ sarà diversa dalla lunghezza misurata in K.
• Questo perché, come abbiamo visto prima, cambia la lunghezza nella direzione del moto, no?
• Sì. Ricordiamo che: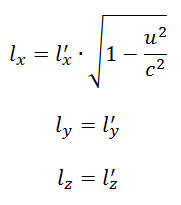quindi la lunghezza di un segmento non è più invariante con il sistema di riferimento. Ma se invece di considerare due punti nello spazio, gli estremi A e B, consideriamo due eventi nello spazio-tempo, vale a dire due eventi che accadono nei punti A e B in due determinati istanti, ritroviamo una invarianza.
• Cioè due eventi descritti dal punto in cui accadono e dal momento in cui accadono?
• Sì, con quattro coordinate, tre spaziali e una temporale. Se consideriamo un evento A e un evento B, e:  a essere invariante è la quantità:chiamata invariante spazio-temporale.
• Invariante nel senso che se misuro queste quantità in qualsiasi riferimento e le inserisco in questa espressione mi viene sempre lo stesso valore?
• Sì. Sostituendo le espressioni delle trasformazioni di Lorentz si ha infatti che:
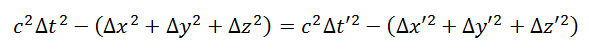
• Cioè non si conserva più la distanza tra due punti ma una sorta di distanza spazio-temporale tra i due eventi.
• Sì, una distanza piuttosto strana, dal momento che se per misurare la distanza tra due punti sommiamo le differenze tra le coordinate spaziali tra i due punti al quadrato (teorema di Pitagora), qui come si può notare si fa una differenza.
• Volendo interpretare la cosa da un punto di vista fisico?
• E’ maledettamente difficile. Possiamo riprendere l’esempio di prima dell’orologio a specchio. Consideriamo i due eventi A e B come, rispettivamente, la partenza del raggio di luce dalla sorgente e il ritorno del raggio di luce alla sorgente. Come sempre avremo, nel sistema di riferimento in cui l’orologio è in moto a velocità u:cioè la distanza spaziale tra i due eventi è:Avremo quindi:Ma abbiamo detto che questa quantità è invariante, quindi si deve avere la stessa espressione se ripetiamo il ragionamento per il sistema in cui l’orologio è in quiete. In questo sistema, gli eventi A e B hanno distanza spaziale nulla (il raggio di luce parte e arriva nello stesso punto) e distanza temporale pari al tempo che impiega il raggio di luce a percorrere la distanza tra specchio e sorgente, e ritorno. 
  Ora, se ricordiamo la relazione che abbiamo trovato prima tra i due intervalli di tempo:otteniamo – come ci si aspettava – proprio l’intervallo invariante calcolato nel sistema di riferimento in moto K’:in cui non compaiono distanze spaziali, avvenendo i due eventi A e B nello stesso punto. Da cui una possibile interpretazione fisica di intervallo invariante. Infatti se facciamo la radice quadrata:vediamo come l’intervallo invariante può essere sempre definito come lo spazio percorso dalla luce nell’intervallo di tempo proprio, cioè nell’intervallo di tempo misurato in un sistema di riferimento in cui gli eventi A e B avvengono nello stesso punto.
• Aspetta un attimo. Proviamo a ritornare a un esempio generico. Consideriamo due eventi A e B osservati da un sistema di riferimento qualsiasi, in cui sono separati spazialmente e temporalmente, cioè hanno coordinate spaziali diverse e avvengono in tempi distinti. Basta trovare un sistema di riferimento, in moto rispetto al precedente, in cui gli eventi hanno le stesse coordinate spaziali, misurare il tempo che intercorre tra i due eventi, e moltiplicarlo per la velocità della luce. Et voilà, quello è l’invariante spazio-temporale. E quel valore sarà identico per qualsivoglia sistema di riferimento…
• Sì. E si può fare anche il contrario, cioè trovare un sistema di riferimento in moto per il quale i due eventi avvengano contemporaneamente, cioè per cui i tempi in cui avvengono A e B sono uguali. In quel caso l’intervallo invariante è la separazione spaziale.
• Mi vengono da pensare due cose: la prima è che in quel caso l’intervallo invariante sarebbe la radice quadrata di un numero negativo…
• Giusto, infatti è proprio quando si ha l’intervallo invariante immaginario che si dice che due eventi sono separati solo spazialmente.
• Ok. La seconda cosa è che, per quanto mi sforzi, nel caso dell’orologio a luce non riesco a trovare un sistema di riferimento per cui A e B avvengano contemporaneamente.
• Vero, infatti è impossibile trovare un sistema di riferimento simile se i due eventi sono in un rapporto di causalità. Nel caso dell’orologio, in cui l’evento B (ritorno alla sorgente) è causato dall’evento A (partenza dalla sorgente), è impossibile trovare un sistema in cui la separazione tra gli eventi sia solo spaziale, e A e B siano contemporanei.
• In questo modo si “tutela” l’ordine di causalità degli eventi quindi! Cioè la Relatività mette in discussione molte cose, ma non questo.
• Sì, sempre che in futuro non escano fuori altre ipotesi al limite del fantascientifico…Come vediamo quindi lo spazio e il tempo sono due aspetti della stessa entità, dal momento che è possibile trovare un sistema di riferimento per cui A e B siano contemporanei ma avvengano in spazi distinti, e un altro per cui avvengano nello stesso luogo ma in tempi diversi (fatte le eccezioni elencate), ma l’intervallo spazio-temporale è sempre lo stesso. E’ un po’ come dire che, per esempio, di un cubo vediamo una sola faccia, o due, o tre a seconda di come orientiamo il sistema di riferimento. In questo senso il tempo è la quarta dimensione.
• Diciamo che ho capito. Ora ci è rimasto di parlare della formula.
• Intendi LA formula?
• Sì.
• Per arrivare adobbiamo premettere che la Relatività prevede che non solo il tempo e lo spazio, ma anche la massa vari al mutare del sistema di riferimento.
• Un’altra cosetta da niente…
• La relazione che lega la massa misurata in un sistema in moto alla massa a riposo è la seguente:
• Vedo che anche qui compare il fattore di Lorentz. Quindi più la massa va veloce e più aumenta. Questo significa anche che più va veloce e più aumenta la propria resistenza all’accelerazione, giusto?
• Sì. E’ ciò che avviene negli acceleratori di particelle, dove sono richieste potenze enormi per accelerare particelle di massa piccolissima. Ora, se riscriviamo la funzione come: 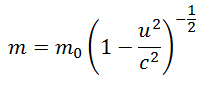e ne facciamo uno sviluppo in serie secondo il teorema binomiale di Newton, otteniamo: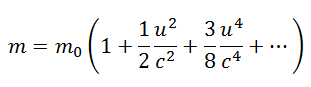di cui supponiamo di trascurare i termini di ordine maggiore, e di fermarci al secondo: 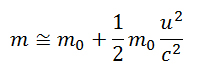Se moltiplichiamo tutto per la velocità della luce al quadrato, otteniamo: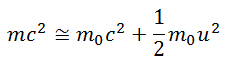
• L’ultimo termine a destra mi sembra familiare…è l’energia cinetica, per quello che ricordo.
• Proprio così. Einstein ebbe l’intuizione di capire che si trovava di fronte all’espressione dell’energia di un corpo, di cui quella cinetica è solo la parte dovuta al moto. Ritornando all’espressione iniziale, abbiamo che quindi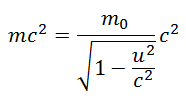è l’energia totale posseduta dalla massa, a riposo se u = 0. Da cui:
• Da cui l’equivalenza massa-energia?
• Sì. La massa si trasforma in energia, e l’energia in massa. Da notare che Einstein aveva intuito di indagare il radio, cioè gli elementi radioattivi – in anticipo enorme sui tempi – con queste parole:

Se un corpo emette l’energia E in forma di radiazione, diminuisce la sua massa di E/c² . È evidentemente inessenziale che l’energia sottratta al corpo sia proprio andata in energia di radiazione, così che siamo condotti alla deduzione più generale: la massa di un corpo è una misura per il suo contenuto di energia. Se varia l’energia E, varia la massa […]. Non e’ escluso che con corpi dei quali il contenuto di energia è variabile in alta misura (per es. con sali di radio) una prova della teoria possa riuscire.

• Pazzesco. Mi pare di capire che abbiamo finito.
• Sì, è stata lunga e dolorosa, ma siamo alla fine.
• Einstein ha partorito la Relatività Generale dieci anni dopo la Ristretta. Speriamo di rivederci prima.
• Speriamo, ma non ci scommetterei.
• Alla prossima.

Ho trovato i concetti fondamentali espressi in questo articolo in due libri di divulgazione, “Sei pezzi meno facili” di R. Feynman e “Il genio e il galantuomo” di F. Toscano, e nell’articolo “Sull’elettrodinamica dei corpi in movimento” di A. Einstein.